Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 146
projektov
Konštrukčná geometria vo vyučovaní matematiky na gymnáziách
| Prípona .rar |
Typ diplomová práca |
Stiahnuté 0 x |
| Veľkosť 0,4 MB |
Jazyk slovenský |
ID projektu 20 |
| Posledná úprava 07.05.2015 |
Zobrazené 7 282 x |
Autor: citron |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
100 Kreditov - kvalita:
92,3% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Katolícka univerzita v Ružomberku
- Fakulta:Pedagogická fakulta
- Kategória:Prírodné vedy » Matematika
- Predmet:-
- Študijný program:-
- Ročník:5. ročník
- Formát:Archív súborov (.rar)
- Rozsah A4:70 strán
Historická poznámka
Kužeľosečkami sa zaoberali vzdelanci už v staroveku. Za ich objaviteľa sa považuje Menaichmos (žil okolo r. 350 pr. n. l.), ktorý ich používal na riešenie problému duplicity kocky. Teóriu kužeľosečiek výrazne obohatil už spomenutý Apollonios z Pergy zadefinovaním združených priemerov, asymptot, dotyčníc a ďalších charakteristických prvkov a ich vlastností vo svojom 8-zväzkovom diele Kužeľosečky bohatom na riešené konštrukčné úlohy. Renesanciu zažili kužeľosečky v XVII. storočí, keď geniálny Johann Kepler (1571 - 1630) a Isaac Newton (1643 - 1727) tieto použili na opis pohybu pla-nét. Vývoj v matematike pokračoval ďalej cestou novoobjavenej súradnicovej sústavy geniálneho filozofa René Descartesa (1596 - 1650) vo forme analytickej geometrie, ktorá spojila až dovtedy nespojiteľné: algebru a geometriu. Fenomenálny piere de Fermat (1601 - 1665) popísal transformácie súradníc posunutím a otočením, pomocou ktorých sa vyšetruje typ kužeľosečiek. Náš kratučký historický exkurz zakončíme u renesančných umelcoch da Vincim a Dürerovi, ktorí pri maľovaní svojich prekrásnych obrazov a stavbe monumentálnych architektonických skvostov používali perspektívu. Títo zobrazovali kružnice do kužeľosečiek, čo matematicky odvodili Garibaldo del Monte (1545 - 1607) a d´Aiguillon (1566- - 1617). Od perspektívy bol už len krok ku Gasparovi Monge (1746 - 1818), ktorý vypracoval teóriu deskriptívnej geometrie premietania na priemetňu a nárysňu…
Poznámka o euklidovských konštrukciách
Spomenutý delský problém duplicity kocky je jedným z klasických gréckych geometrických problémov/úloh (trisekcia uhla, kvadratúra kruhu, rektifikácia kružnice, konštrukcia pravidelných n-uholníkov, duplicita kocky). Snahy o ich vyriešenie obohatili matematiku o mnohé poznatky a postupy. Okrem iného niektorí učenci zostrojovali dômyselné mechanizmy (napr. tzv. križiak) na rysovanie rôznych kriviek (napr. kvadratrix), keď tieto nedokázali presne narysovať pomocou lineára a kružidla.
Vplyvom Platóna (427 - 347 pr. n. l.) a jeho idealistickej filozofie došlo k zavrhnutiu týchto mechanických pomôcok aj kriviek, ktoré sa nimi konštruovali. Platón si totiž matematiku vysoko považoval a matematické pojmy vyhlásil za akéhosi sprostredkovateľa sveta ideí a fyzického sveta. Preto nástojil, aby sa matematika venovala len ideálne dokonalému a pravidelnému, čo nepodlieha zmene - presne tak ako večné, dokonalé, nehybné a stále idey. Z toho dôvodu sa na jeho Akadémii (zal. r. 387 pr. n. l.) študovali len pravidelné rovinné a priestorové útvary: kružnice a guľové plochy, priamky a roviny, ktoré je možné konštruovať za pomocou lineára a kružidla. Jedine tieto mechanické pomôcky považoval za vhodné pre geometrické konštrukcie, pretože útvary nimi skonštruované sú ideálne: sú dokonale súmerné a schopné pohybu sami v sebe (a pri tomto pohybe sa nemenia, sú stále, ako idey).
Tieto názory si pre silný vplyv osvojili i vtedajší grécki matematici, medzi nimi aj Euklides, ktorý napísal Základy - až do novoveku jedinú a všetkými akceptovanú učebnicu geometrie. Hoci to výslovne nikde
neuvádza, pri konštrukciách používa výhradne lineár a kružidlo (viac z histórie matematiky pozri napr. v [4], s. 262 - 294).
Kužeľosečkami sa zaoberali vzdelanci už v staroveku. Za ich objaviteľa sa považuje Menaichmos (žil okolo r. 350 pr. n. l.), ktorý ich používal na riešenie problému duplicity kocky. Teóriu kužeľosečiek výrazne obohatil už spomenutý Apollonios z Pergy zadefinovaním združených priemerov, asymptot, dotyčníc a ďalších charakteristických prvkov a ich vlastností vo svojom 8-zväzkovom diele Kužeľosečky bohatom na riešené konštrukčné úlohy. Renesanciu zažili kužeľosečky v XVII. storočí, keď geniálny Johann Kepler (1571 - 1630) a Isaac Newton (1643 - 1727) tieto použili na opis pohybu pla-nét. Vývoj v matematike pokračoval ďalej cestou novoobjavenej súradnicovej sústavy geniálneho filozofa René Descartesa (1596 - 1650) vo forme analytickej geometrie, ktorá spojila až dovtedy nespojiteľné: algebru a geometriu. Fenomenálny piere de Fermat (1601 - 1665) popísal transformácie súradníc posunutím a otočením, pomocou ktorých sa vyšetruje typ kužeľosečiek. Náš kratučký historický exkurz zakončíme u renesančných umelcoch da Vincim a Dürerovi, ktorí pri maľovaní svojich prekrásnych obrazov a stavbe monumentálnych architektonických skvostov používali perspektívu. Títo zobrazovali kružnice do kužeľosečiek, čo matematicky odvodili Garibaldo del Monte (1545 - 1607) a d´Aiguillon (1566- - 1617). Od perspektívy bol už len krok ku Gasparovi Monge (1746 - 1818), ktorý vypracoval teóriu deskriptívnej geometrie premietania na priemetňu a nárysňu…
Poznámka o euklidovských konštrukciách
Spomenutý delský problém duplicity kocky je jedným z klasických gréckych geometrických problémov/úloh (trisekcia uhla, kvadratúra kruhu, rektifikácia kružnice, konštrukcia pravidelných n-uholníkov, duplicita kocky). Snahy o ich vyriešenie obohatili matematiku o mnohé poznatky a postupy. Okrem iného niektorí učenci zostrojovali dômyselné mechanizmy (napr. tzv. križiak) na rysovanie rôznych kriviek (napr. kvadratrix), keď tieto nedokázali presne narysovať pomocou lineára a kružidla.
Vplyvom Platóna (427 - 347 pr. n. l.) a jeho idealistickej filozofie došlo k zavrhnutiu týchto mechanických pomôcok aj kriviek, ktoré sa nimi konštruovali. Platón si totiž matematiku vysoko považoval a matematické pojmy vyhlásil za akéhosi sprostredkovateľa sveta ideí a fyzického sveta. Preto nástojil, aby sa matematika venovala len ideálne dokonalému a pravidelnému, čo nepodlieha zmene - presne tak ako večné, dokonalé, nehybné a stále idey. Z toho dôvodu sa na jeho Akadémii (zal. r. 387 pr. n. l.) študovali len pravidelné rovinné a priestorové útvary: kružnice a guľové plochy, priamky a roviny, ktoré je možné konštruovať za pomocou lineára a kružidla. Jedine tieto mechanické pomôcky považoval za vhodné pre geometrické konštrukcie, pretože útvary nimi skonštruované sú ideálne: sú dokonale súmerné a schopné pohybu sami v sebe (a pri tomto pohybe sa nemenia, sú stále, ako idey).
Tieto názory si pre silný vplyv osvojili i vtedajší grécki matematici, medzi nimi aj Euklides, ktorý napísal Základy - až do novoveku jedinú a všetkými akceptovanú učebnicu geometrie. Hoci to výslovne nikde
neuvádza, pri konštrukciách používa výhradne lineár a kružidlo (viac z histórie matematiky pozri napr. v [4], s. 262 - 294).
Kľúčové slová:
Konštrukcia
Metodika
Terminológia
Elipsa
Definécia
Priamka
Dotyčnica
Tangenta
Kružnica
Hyperbola
Prvok
Bod
Asymptota
Obsah:
- 0. Úvodné poznámky o kužeľosečkách 8
Historická poznámka 9
Poznámka o euklidovských konštrukciách 10
Poznámka o riešení konštrukčných úloh 11
Metodika práce (s naším učebným textom) 12
Poznámka o terminológii 13
1. Elipsa 15
1.1. Konštrukcia elipsy a jej charakteristické prvky 15
1.2. Bod a elipsa 22
Riešené úlohy (1) 22
Neriešené úlohy (2) 24
1.3. Priamka a elipsa 25
1.3.1. Dotyčnica (tangenta) elipsy 25
1.4. Riadiaca kružnica (directrix) elipsy 28
1.5. Vrcholová kružnica elipsy 29
Riešené úlohy (2) 32
Neriešené úlohy (2) 33
2. Hyperbola 34
2.1. Konštrukcia hyperboly a jej charakteristické prvky 34
2.2. Bod a hyperbola 39
Riešené úlohy (3) 40
Neriešené úlohy (3) 41
2.3. Priamka a hyperbola 41
2.3.1. Dotyčnica (tangenta) hyperboly 42
2.3.2. Asymptoty hyperboly 43
2.4. Riadiaca kružnica (directrix) hyperboly 44
2.5. Vrcholová kružnica hyperboly 46
Riešené úlohy (4) 49
Neriešené úlohy (4) 50
3. Parabola 51
3.1. Konštrukcia paraboly a jej charakteristické prvky 51
3.2. Bod a parabola 52
Riešené úlohy (5) 53
Neriešené úlohy (5) 53
3.3. Priamka a parabola 54
3.3.1. Dotyčnica (tangenta) paraboly 54
3.4. Riadiaca priamka (directrix) paraboly 56
3.5. Vrcholová dotyčnica paraboly 56
Riešené úlohy (6) 60
Neriešené úlohy (6) 63
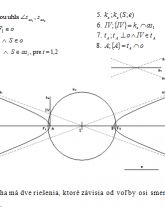
4. Spoločná ohnisková definícia kužeľosečiek 65
ZÁVER 66
POUŽITÁ LITERATÚRA A PRAMENE 67
Zdroje:
- Hlavná literatúra
- Husarčík, J. - Kaštieľ, M.: Inžinierska geometria. Žilina: vydala vysoká škola dopravy a spojov v Žiline, 1994.
- Medek, V. - Zámožík, J.: Deskriptívna geometria pre technikov. Bratislava: Alfa, 1978.
- Medek, V. - Zámožík, J.: Deskriptívna geometria, príklady a úlohy. Bratislava: Alfa, 1985.
- Oravec, G. - Rybár, J. - Šulka, R.: Deskriptívna geometria I. Bratislava: vydala Slovenská vysoká škola technická v Bratislave v edičnom stredisku SVŠT, 1983.
- Senko, E.: Deskriptívna geometria. Zvolen: vydala Vysoká škola lesnícka a drevárska vo Zvolene v edičnom stredisku VŠLD, 1976.
- Šedivý, O. - Hamalová, E.: Deskriptívna geometria. Bratislava: vydala Pedagogická fakulta v Nitre v SPN, 1971.
- Višňanský, R.: Deskriptívna geometria I. Žilina: vydala Žilinská univerzita v Žiline, 1999.
- Hejný, M. a kol.: Teória vyučovania matematiky 2. Bratislava: SPN, 1989.
- Pavlič, G.: Školská encyklopédia matematiky. Bratislava: Príroda, 2001.
- Sekanina, M. et al.: Geometrie II. Praha: SPN, 1988.
- Šofr, B.: Euklidovské geometrické konštrukcie. Bratislava: Alfa, 1976.
- Ladislav Kvasz, L.: Prvky algebraického myslenia v antickej matematike. článok dostupný na http://www.matika.sk
- kol. autorov: Geometria 2. Bratislava: SPN, 1987.
- Pomocná literatúra
- Gallo, O. - Kuniak, M. - Paluch V.: Deskriptívna geometria. Bratislava: Alfa, 1971.
- Deskriptívna geometria pre 2. a 3. ročník SVŠ. Bratislava: SPN, 1965.
- Gallo, O. - Paluch, V.: Konštrukčná geometria pre poslucháčov strojníckej fakulty. Bratislava: Alfa, 1983.
- Klimčík, J.: Deskriptívna geometria I. Bratislava: Alfa, 1980.
- Maroszová, G.: Konštrukčná geometria. Banská Bystrica: Univerzita Mateja Bella, 1993.
- Novotný, Š. - Švec, O.: Deskriptívna geometria. Nitra: vydala Vysoká škola poľnohospodárska v Nitre, 2. vydanie, 1979.
- Frecerová, J.: Deskriptívna geometria, riešenia základných úloh. Bratislava: SVŠT v Bratislave, 1980.
- Frecerová, J.- Čižmárová, B. - Píšová, F.: Inžinierska geometria, riešené príklady. Bratislava: STU v Bratislave, 2000.
- Machová, B. et al.: Deskriptívna geometria v príkladoch. Bratislava: Slovenské vydavateľstvo technickej literatúry, 1959.
- Palajová, H.: Zbierka úloh z deskriptívnej geometrie. Zvolen: MAT-Centrum, 1997.
- Rybár, J. - Oravec, G. et al.: Deskriptívna geometria (úlohy a cvičenia). Bratislava: SVŠT, 1988.
- Švec, O.: Deskriptívna geometria, návody na cvičenia. Nitra: Slovenská poľnohospodárska univerzita v Nitre vo vydavateľskom a edičnom stre-disku SPU, 2000.