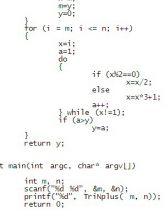Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 144
projektov
Základy informatika - Q - 3n+1 - pre expertov
| Prípona .doc |
Typ počítačové zadanie |
Stiahnuté 2 x |
| Veľkosť 0,1 MB |
Jazyk slovenský |
ID projektu 2036 |
| Posledná úprava 06.09.2016 |
Zobrazené 1 478 x |
Autor: xxmiloss |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
2 Kreditov - kvalita:
76,7% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Trenčianska univerzita Alexandra Dubčeka v Trenčíne
- Fakulta:Fakulta mechatroniky
- Kategória:Technika » Informatika
- Predmet:Základy informatiky
- Študijný program:-
- Ročník:1. ročník
- Formát:MS Office Word (.doc)
- Rozsah A4:1 strán
Uvažujme nasledujúci algoritmus, ktorý generuje postupnosť čísel. Začína sa od celého čísla n. Ak je n párne, delí sa číslom 2. Ak je n nepárne, vynásobí sa číslom 3 a pripočíta sa 1. Toto sa opakuje, pokiaľ n nie je 1. Napríklad nasledujúca postupnosť čísel je vygenerovaná z čísla 22.
22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
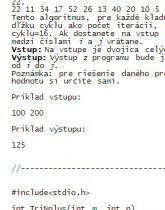
Tento algoritmus, pre každé kladné celé číslo skončí keď n=1. Pre dané n môžeme definovať dĺžku cyklu ako počet iterácií, pokiaľ nebude n=1. Pre predchádzajúci príklad (n=22) je dĺžka cyklu=16. Ak dostanete na vstup dve čísla i a j, máte za úlohu zistiť najdlhšiu dĺžku cyklu medzi číslami i a j vrátane.
Vstup: Na vstupe je dvojica celých čísel i a j. Obe čísla sú menšie ako 32 000 a väčšie ako 0. Výstup: Výstup z programu bude jedno číslo, ktoré reprezentuje maximálnu dĺžku cyklu pre čísla od i do j.
Poznámka: pre riešenie daného problému vytvorte funkciu TriNplus(). Paramatre a návratovú hodnotu si určite sami.
Príklad vstupu:
100 200
Príklad výstupu:
125
22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
Tento algoritmus, pre každé kladné celé číslo skončí keď n=1. Pre dané n môžeme definovať dĺžku cyklu ako počet iterácií, pokiaľ nebude n=1. Pre predchádzajúci príklad (n=22) je dĺžka cyklu=16. Ak dostanete na vstup dve čísla i a j, máte za úlohu zistiť najdlhšiu dĺžku cyklu medzi číslami i a j vrátane.
Vstup: Na vstupe je dvojica celých čísel i a j. Obe čísla sú menšie ako 32 000 a väčšie ako 0. Výstup: Výstup z programu bude jedno číslo, ktoré reprezentuje maximálnu dĺžku cyklu pre čísla od i do j.
Poznámka: pre riešenie daného problému vytvorte funkciu TriNplus(). Paramatre a návratovú hodnotu si určite sami.
Príklad vstupu:
100 200
Príklad výstupu:
125
Kľúčové slová: