Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 119
projektov
Algebra a diskrétna matematika
«»
| Prípona |
Typ prednášky |
Stiahnuté 6 x |
| Veľkosť 0,4 MB |
Jazyk slovenský |
ID projektu 10668 |
| Posledná úprava 11.06.2019 |
Zobrazené 2 671 x |
Autor: - |
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
10 Kreditov - kvalita:
89,2% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Slovenská technická univerzita v Bratislave
- Fakulta:Fakulta informatiky a informačných technológií
- Kategória:Technika » Informatika
- Predmet:Algebra a diskrétna matematika
- Študijný program:-
- Ročník:1. ročník
- Formát:PDF dokument (.pdf)
- Rozsah A4:62 strán
Význam dôkazu v matematike
V matematike, podobne ako aj v informatike, vystupujú do popredia dve otázky:
(1) Za akých podmienok je matematický argument korektný a
(2) aké metódy môžu byť použité pri konštrukcii matematických argumentov.
Veta (teorém, výrok, skutočnosť, fakt, alebo výsledok) je výrok o ktorom môže byť ukázané, že je pravdivý.
Dôkaz vety - je postupnosť argumentov, ktoré sú odvodené buď z množiny jednoduchých argumentov - postulátov, nazývaných axiómy, alebo z predchádzajúcich argumentov (pomocných viet, často nazývané lemy) danej postupnosti.
Postupnosť argumentov môže byť podstatne skrátená, keď bude obsahovať už dokázané vety, ktoré sú založené na rovnakej množine axióm.
V matematike, podobne ako aj v informatike, vystupujú do popredia dve otázky:
(1) Za akých podmienok je matematický argument korektný a
(2) aké metódy môžu byť použité pri konštrukcii matematických argumentov.
Veta (teorém, výrok, skutočnosť, fakt, alebo výsledok) je výrok o ktorom môže byť ukázané, že je pravdivý.
Dôkaz vety - je postupnosť argumentov, ktoré sú odvodené buď z množiny jednoduchých argumentov - postulátov, nazývaných axiómy, alebo z predchádzajúcich argumentov (pomocných viet, často nazývané lemy) danej postupnosti.
Postupnosť argumentov môže byť podstatne skrátená, keď bude obsahovať už dokázané vety, ktoré sú založené na rovnakej množine axióm.
Kľúčové slová:
algebra
diskrétna matematika
výroková logika
univerzálny kvantifikátor
dôkaz sporom
matematická indukcia
deduktívny dôkaz
existenčný kvantifikátor
Obsah:
- Metódy matematického dôkazu
Význam dôkazu v matematike
Deduktívny dôkaz
Induktívne usudzovanie
Ilustračný príklad axiomatického systému
Pravidlá usudzovania vo výrokovej logike
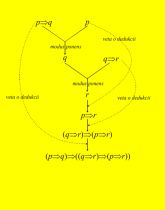
Diagramatická reprezentácia príkladu
Veta o dedukcii
Chybné pravidlá usudzovania
Pravidlá usudzovania v predikátovej logike
Konkretizácia univerzálneho kvantifikátora
Zovšeobecnenie pomocou univerzálneho kvantifikátora
Konkretizácia existenčného kvantifikátora
Zovšeobecnenie pomocou existenčného kvantifikátora
Metódy dôkazu viet
Matematická indukcia
Silná matematická indukcia
Pridaj projekt
Pridaj projekt a získaj kredity za stiahnutie. S kreditmi možeš sťahovať iné projekty. Je to jednoduché :)
Najčastejšie
Zobraz
Odporúčame
Zadania-seminarky.sk
2006 - 2024 © všetky práva vyhradené