Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 144
projektov
Konštruktívna geometria - komplet prednášky
| Prípona .zip |
Typ prednášky |
Stiahnuté 1 x |
| Veľkosť 3,3 MB |
Jazyk slovenský |
ID projektu 45969 |
| Posledná úprava 22.06.2015 |
Zobrazené 1 457 x |
Autor: igor6669 |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
20 Kreditov - kvalita:
89,6% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Trenčianska univerzita Alexandra Dubčeka v Trenčíne
- Fakulta:Fakulta špeciálnej techniky
- Kategória:Technika » Strojárstvo
- Predmet:Konštruktívna geometria
- Študijný program:Servis a opravy automobilov
- Ročník:1. ročník
- Formát:Archív súborov (.zip)
- Rozsah A4:89 strán
Rozšírenie euklidovského priestoru o nevlastné elementy
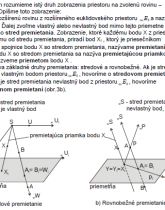
Smer každej priamky q z euklidovského priestoru budeme nazývať nevlastným bodom tejto priamky (budeme ho označovať ∞) a pridaním tohto nového (jediného nového) bodu na priamku q získame rozšírenú priamku q. 3EQQ∞
Priamky navzájom rovnobežné (t.j. priamky toho istého smeru) sú po ich rozšírení priamkami so spoločným nevlastným bodom, dve nerovnobežné priamky rozšírené o svoje nevlastné body majú tieto nevlastné body rôzne (obr.1a).
Každá rovina z euklidovského priestoru bude takto rozšírená o množinu nevlastných bodov ležiacich na jej rozšírených priamkach . Množinu všetkých nevlastných bodov, ktoré do roviny a prinášajú jej rozšírené priamky, nazveme nevlastnou priamkou roviny a , označovať ju budeme (obr.1b).
Smer každej priamky q z euklidovského priestoru budeme nazývať nevlastným bodom tejto priamky (budeme ho označovať ∞) a pridaním tohto nového (jediného nového) bodu na priamku q získame rozšírenú priamku q. 3EQQ∞
Priamky navzájom rovnobežné (t.j. priamky toho istého smeru) sú po ich rozšírení priamkami so spoločným nevlastným bodom, dve nerovnobežné priamky rozšírené o svoje nevlastné body majú tieto nevlastné body rôzne (obr.1a).
Každá rovina z euklidovského priestoru bude takto rozšírená o množinu nevlastných bodov ležiacich na jej rozšírených priamkach . Množinu všetkých nevlastných bodov, ktoré do roviny a prinášajú jej rozšírené priamky, nazveme nevlastnou priamkou roviny a , označovať ju budeme (obr.1b).
Kľúčové slová:
geometria
nevlastné prvky
axonometria
krivky
plochy
Obsah:
- 1. nevlastné prvky
2. premietanie
3. perspektívna afinita
4. mongeova projekcia
5. axonometria
6. základné polohové úlohy
7.metrické úlohy
8. elementárne plochy a telesá
9. krivky
10. plochy
11. rotačné plochy
12. špeciálne typy rotačných plôch
13. skrutkové plochy