Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 146
projektov
Matematika 2 - priebeh funkcie a derivácia funkcie
| Prípona .doc |
Typ prednášky |
Stiahnuté 9 x |
| Veľkosť 0,3 MB |
Jazyk slovenský |
ID projektu 6611 |
| Posledná úprava 09.08.2018 |
Zobrazené 2 624 x |
Autor: - |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
5 Kreditov - kvalita:
86,3% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Žilinská univerzita v Žiline
- Fakulta:Fakulta špeciálneho inžinierstva
- Kategória:Prírodné vedy » Matematika
- Predmet:Matematika 2
- Študijný program:-
- Ročník:1. ročník
- Formát:MS Office Word (.doc)
- Rozsah A4:6 strán
Konvexnosť a konkávnosť funkcie.
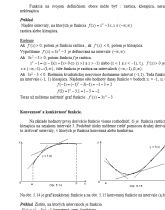
Na základe hodnoty prvej derivácie funkcie vieme rozhodnúť, či je funkcia rastúca lebo klesajúca na nejakom intervale J. Podobné úlohy môžeme riešiť pomocou druhej derivácie, a to zisťovať intervaly, v ktorých je funkcia konvexná alebo konkávna.
Lokálne extrémy funkce (maximum a minimum funkcie)
V aplikáciách matematiky sa často vyskytuje úloha nájsť najväčšiu alebo najmenšiu hodnotu funkcie a určiť tie body z jej definičného oboru, v ktorých tieto hodnoty nadobúda. Môže ísť o najväčšiu alebo najmenšiu hodnotu v celom definičnom obore, alebo iba v nejakom okolí daného bodu. Lokálne maximá, minimá funkcie f majú spoločný názov lokálne extrémy funkcie f. Bod, v ktorom má funkcia lokálny extrém, sa nazýva bod lokálneho extrému.. Ak má funkcia f v bode x0 lokálny extrém a má v tomto bode deriváciu f´(x0), tak Táto podmienka je nutná k tomu, aby funkcia f, ktorá má v bode x0 deriváciu, mala v bode x0 lokálny extrém. Ak je hodnota druhej derivácie v tomto bode vačšia ako nula ide o lokalne minimum , ak je menšia ako nula ide o lokálne maximum.
Na základe hodnoty prvej derivácie funkcie vieme rozhodnúť, či je funkcia rastúca lebo klesajúca na nejakom intervale J. Podobné úlohy môžeme riešiť pomocou druhej derivácie, a to zisťovať intervaly, v ktorých je funkcia konvexná alebo konkávna.
Lokálne extrémy funkce (maximum a minimum funkcie)
V aplikáciách matematiky sa často vyskytuje úloha nájsť najväčšiu alebo najmenšiu hodnotu funkcie a určiť tie body z jej definičného oboru, v ktorých tieto hodnoty nadobúda. Môže ísť o najväčšiu alebo najmenšiu hodnotu v celom definičnom obore, alebo iba v nejakom okolí daného bodu. Lokálne maximá, minimá funkcie f majú spoločný názov lokálne extrémy funkcie f. Bod, v ktorom má funkcia lokálny extrém, sa nazýva bod lokálneho extrému.. Ak má funkcia f v bode x0 lokálny extrém a má v tomto bode deriváciu f´(x0), tak Táto podmienka je nutná k tomu, aby funkcia f, ktorá má v bode x0 deriváciu, mala v bode x0 lokálny extrém. Ak je hodnota druhej derivácie v tomto bode vačšia ako nula ide o lokalne minimum , ak je menšia ako nula ide o lokálne maximum.
Kľúčové slová:
funkcie
derivácia
konvexnosť
konkávnosť
monotónnosť
lokálne extrémy
priebeh funkcie
matematika
exponenciálne funkcie
Obsah:
- Derivácia funkcie
Základné pravidlá derivovania
Derivácie elementárnych funkcií
Príklady na derivovanie funkcií
Monotónnosť funkcie
Konvexnosť a konkávnosť funkcie
Lokálne extrémy funkce (maximum a minimum funkcie)
Všeobecná schéma pre vyšetrovanie priebehu funkcie
Graf funkcie