Home » Skriptá » Komplexné čísla a algebraické rovnice

Komplexné čísla a algebraické rovnice

«»

Prípona .pdf	Typ skriptá	Stiahnuté 31 x
Veľkosť 0,2 MB	Jazyk slovenský	ID projektu 2139
Posledná úprava 25.09.2016	Zobrazené 1 648 x	Autor: -
Zdieľaj na Facebooku
Detaily projektu

cena:
5 Kreditov
kvalita:
73,6%
73,6%
Stiahni
Pridaj na porovnanie

Univerzita:-
Fakulta:-
Kategória:Prírodné vedy » Matematika
Predmet:Matematika
Študijný program:-
Ročník:-
Formát:PDF dokument (.pdf)
Rozsah A4:10 strán

Popis:

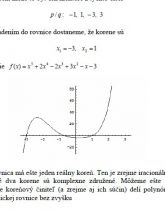
Vieme, že existujú kvadratické rovnice, ktoré nemajú riešenie v obore reálnych čísel. Sú to také, ktorých diskriminant je záporný. Uvažujme kvadratickú rovnicu

x2 − 2x + 5 = 0

Použitím štandardnej formule pre výpočet koreňov kvadratickej rovnice dostaneme

Hovoríme, že táto rovnica nemá riešenie v obore reálnych čísel. Zavedieme nové "číslo" i (imaginárna jednotka), ktoré vyhovuje podmienke

Čísla tohto typu budeme nazývať komplexné čísla.
Kvadratická rovnica má vždy riešenie v obore komplexných čísel. Komplexné číslo má teda tvar

z = x + iy

Kľúčové slová:

komplexné čísla

diskrimiinant

kvadratické rovnice

reálne čísla

polynómy

algebraické rovnice

Obsah:

4. Komplexné čísla a algebraické rovnice
4.1 Komplexné čísla
4.2 Operácie s komplexnými číslami
4.3 Polynómy a algebraické rovnice

Zdieľaj na Facebooku

Stiahni

Pridaj projekt

Pridaj projekt a získaj kredity za stiahnutie. S kreditmi možeš sťahovať iné projekty. Je to jednoduché :)

Najčastejšie

Zobraz

Odporúčame