Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 118
projektov
Aplikovaná matematika - ťahák
«»
| Prípona .docx |
Typ ťahák |
Stiahnuté 14 x |
| Veľkosť 0,2 MB |
Jazyk slovenský |
ID projektu 43351 |
| Posledná úprava 05.02.2014 |
Zobrazené 2 107 x |
Autor: patto2008 |
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
6 Kreditov - kvalita:
82,9% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Technická univerzita v Košiciach
- Fakulta:Fakulta výrobných technológií so sídlom v Prešove
- Kategória:Technika » Strojárstvo
- Predmet:Aplikovaná matematika
- Študijný program:Počítačová podpora výrobných technológií
- Ročník:4. ročník
- Formát:MS Office Word (.docx)
- Rozsah A4:3 strán
5. Newtonova metóda
Separácia koreňov rovnice - tabelaciou funkcii viac premenných alebo grafickým riešením sústav rovníc.
Grafické riešenie nelineárnej rovnice:
- Reálne korene rovnice f(x)=0 určíme graficky ako x-ové súradnice priesečníkov grafu funkcie f(x) s osou x v pravouhlom súradnicovom systéme
- Alebo rovnicu f(x) nahradíme rovnicou a potom reálne korene sú x-ové súradnice priesečníkov funkcii a
Cauchyho veta - Nech funkcia f: R É A ® R je spojitá na intervale Ì A a platí f(a).f(b) < 0 Potom existuje aspoň jedno číslo c Î (a, b) také, že f(c) = 0 Newtonová metóda: Nech f(x) splna podmienky Cauchyho vety, potom existuje koreň rovnice f(x) = 0 na intervale pričom za x0 volíme a, b podľa podmienky Zvolíme začiatočné priblíženie podľa podmienky Vypočítame členy postupnosti Ak máme vypočítať koreň a s vopred zadanou presnosťou e, výpočet ukončíme, keď je splnená podmienka Pričom a položíme rovné
Separácia koreňov rovnice - tabelaciou funkcii viac premenných alebo grafickým riešením sústav rovníc.
Grafické riešenie nelineárnej rovnice:
- Reálne korene rovnice f(x)=0 určíme graficky ako x-ové súradnice priesečníkov grafu funkcie f(x) s osou x v pravouhlom súradnicovom systéme
- Alebo rovnicu f(x) nahradíme rovnicou a potom reálne korene sú x-ové súradnice priesečníkov funkcii a
Cauchyho veta - Nech funkcia f: R É A ® R je spojitá na intervale Ì A a platí f(a).f(b) < 0 Potom existuje aspoň jedno číslo c Î (a, b) také, že f(c) = 0 Newtonová metóda: Nech f(x) splna podmienky Cauchyho vety, potom existuje koreň rovnice f(x) = 0 na intervale pričom za x0 volíme a, b podľa podmienky Zvolíme začiatočné priblíženie podľa podmienky Vypočítame členy postupnosti Ak máme vypočítať koreň a s vopred zadanou presnosťou e, výpočet ukončíme, keď je splnená podmienka Pričom a položíme rovné
Kľúčové slová:
Newtonov interpolačný polynóm
Lagrangeov interpolačný polynóm
interačná metóda
Jacobiho metóda
metóda regula-falsi
metóda bisekcie
Obsah:
- 1.Newtonov interpolačný polynóm
2. Lagrangeov interpolačný polynóm
3. Metoda najmenších štvorcov
4. Metoda bisekcie
5. Newtonova metóda
6. Metoda regula-falsi
7. Interačná metóda
8. Jacobiho metóda na riešenie sústavy lineárnych rovníc
9. Interačná metóda na riešenie sústavy nelineárnych rovníc
10. Gauss - Seidelová metóda
11. Newtonova metóda na riešenie sústavy nelineárnych rovníc
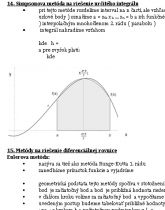
12. Obdĺžniková metóda na riešenie určitého integrálu
13. Lichobežníková metóda na riešenie určitého integrálu
14. Simpsonova metóda na riešenie určitého integrálu
15. Metódy na riešenie diferenciálnej rovnice
16. Metódy na riešenie diferenciálnej rovnice
17. Základne charakteristiky jednorozmerného štatistického súboru
18. Početnosti a grafické znázornenie štatistického súboru
19. Náhodná premenná. Diskrétna a spojitá náhodná premenná
20. Diskrétne rozdelenie pravdepodobnosti
21. Spojite rozdelenie pravdepodobnosti
22. Testovanie štatistických hypotéz
Pridaj projekt
Pridaj projekt a získaj kredity za stiahnutie. S kreditmi možeš sťahovať iné projekty. Je to jednoduché :)
Najčastejšie
Zobraz
Odporúčame
Zadania-seminarky.sk
2006 - 2024 © všetky práva vyhradené