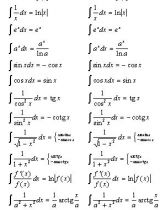Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 144
projektov
Matematika A - ťahák
| Prípona .zip |
Typ ťahák |
Stiahnuté 3 x |
| Veľkosť 0,1 MB |
Jazyk slovenský |
ID projektu 43740 |
| Posledná úprava 27.12.2013 |
Zobrazené 1 611 x |
Autor: barbora |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
1 Kreditov - kvalita:
75,6% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Ekonomická univerzita v Bratislave
- Fakulta:Fakulta podnikového manažmentu
- Kategória:Prírodné vedy » Matematika
- Predmet:Matematika A
- Študijný program:Manažment
- Ročník:2. ročník
- Formát:Archív súborov (.zip)
- Rozsah A4:4 strán
Funkcia jednej reálnej premennej:
1. Nech A je neprázdna množina. Zobrazenie f množiny A do množiny R nazývame reálnou funkciou. Reálna funkcia je teda zobrazenie f: AR, ktoré každému prvku xA priradí jediné reálne číslo y=f(x).
2. Reálnu funkciu f: AR, AR nazývame reálnou funkciou jednej reálnej premennej.
3. Ak f: AR je funkcia, tak množína A sa nazýva definičný obor funkcie f a označuje sa znakom D(f) a množina f(A)=yR y=f(x), xA sa nazýva obor hodnôt funkcie f a označuje sa H(f).
4. Z definície ohraničenosti množiny zdola, zhora vyplýva, že funkcia f je zhora (zdola) ohraničená na množine A práve vtedy, ak existuje také reálne číslo k[h], že pre všetky xA platí: f(x)k (f(x)h). Analogicky dostaneme, že funkcia f je ohraničená na množine A, práve vtedy, ak existuje číslo K0, že platí f(x)K, pre každé xA.
5. Funkcia f je párna (nepárna) na množine AD(f), ak pre každé xA je tiež -xA a platí f(x)=f(-x) [f(-x)=-f(x)].
6. Funkciu f nazývame periodickou, ak existuje také kladné číslo p0, že platí: a) xD(f)x+pD(f), b) pre každé xD(f) je f(x+p)=f(x).
7. Funkciu f nazývame prostou na množine A, ak pre každé dva body x1, x2A, x1x2, platí f(x1)f(x2).
8. Nech funkcia f je prostá na množine AD(f). Potom inverznou funkciou f -1 definovanou na množine f(A) k funkcii f definovanej na A, nazývame predpis, podľa ktorého každému prvku xf(A) priradíme prvok yA, tak že f(y)=x. Ak A=D(f), hovoríme o inverznej funkcii k funkcii f. Zo vzťahov f(y)=x a y=f -1(x) dostávame: xf(A):f(f -1(x))=x, yA:f -1(f(y))=y.
1. Nech A je neprázdna množina. Zobrazenie f množiny A do množiny R nazývame reálnou funkciou. Reálna funkcia je teda zobrazenie f: AR, ktoré každému prvku xA priradí jediné reálne číslo y=f(x).
2. Reálnu funkciu f: AR, AR nazývame reálnou funkciou jednej reálnej premennej.
3. Ak f: AR je funkcia, tak množína A sa nazýva definičný obor funkcie f a označuje sa znakom D(f) a množina f(A)=yR y=f(x), xA sa nazýva obor hodnôt funkcie f a označuje sa H(f).
4. Z definície ohraničenosti množiny zdola, zhora vyplýva, že funkcia f je zhora (zdola) ohraničená na množine A práve vtedy, ak existuje také reálne číslo k[h], že pre všetky xA platí: f(x)k (f(x)h). Analogicky dostaneme, že funkcia f je ohraničená na množine A, práve vtedy, ak existuje číslo K0, že platí f(x)K, pre každé xA.
5. Funkcia f je párna (nepárna) na množine AD(f), ak pre každé xA je tiež -xA a platí f(x)=f(-x) [f(-x)=-f(x)].
6. Funkciu f nazývame periodickou, ak existuje také kladné číslo p0, že platí: a) xD(f)x+pD(f), b) pre každé xD(f) je f(x+p)=f(x).
7. Funkciu f nazývame prostou na množine A, ak pre každé dva body x1, x2A, x1x2, platí f(x1)f(x2).
8. Nech funkcia f je prostá na množine AD(f). Potom inverznou funkciou f -1 definovanou na množine f(A) k funkcii f definovanej na A, nazývame predpis, podľa ktorého každému prvku xf(A) priradíme prvok yA, tak že f(y)=x. Ak A=D(f), hovoríme o inverznej funkcii k funkcii f. Zo vzťahov f(y)=x a y=f -1(x) dostávame: xf(A):f(f -1(x))=x, yA:f -1(f(y))=y.
Kľúčové slová:
limity funkcie
spojitosť funkcie
diferenciál funkcie
nevlastný integrál
Obsah:
- Matematika A
Matematika A - teória
Tabuľkové integrály