Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 144
projektov
Optimalizácia - vypracovanie zadaní
| Prípona .zip |
Typ výpočet |
Stiahnuté 1 x |
| Veľkosť 1,1 MB |
Jazyk slovenský |
ID projektu 2041 |
| Posledná úprava 06.09.2016 |
Zobrazené 1 929 x |
Autor: riverman |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
12 Kreditov - kvalita:
77,4% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Slovenská technická univerzita v Bratislave
- Fakulta:Fakulta elektrotechniky a informatiky
- Kategória:Prírodné vedy » Matematika
- Predmet:Optimalizácia
- Študijný program:-
- Ročník:-
- Formát:Archív súborov (.zip)
- Rozsah A4:42 strán
1.Nájdite lokálny extrém funkcie f(x) =4x3−8x2−4x+2
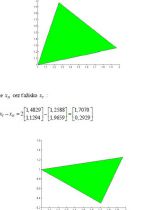
1.Nájdite minimum funkcie f (u,v) =u2+2u−4uv+5v2−8v+5 metódou Neldera
a Meada ( 4 kroky ). Vrcholy východiskového simplexu :
(1.9659,1.2588);(1.2588,1.9659);(1,1).
1. Riešte úlohu: extr f x y x y
x y
( , ) 4 2
,
= + pri splnení ohraničenia: x2 + y2 = 2 (extr znamená
minimum alebo maximum). Ako sa zmení optimálna hodnota f(x,y), ak sa pravá strana
ohraničenia zmení na 1. Nakreslite.
Prípravok na podlahu má vzniknúť vhodnou kombináciou troch surovín, obsahujúcich
čistiace - C, dezinfekčné - D a neutrálne - N, ako aj alergiu -vyvolávajúce - A zložky; ich
obsah je uvedený v tabuľke. Požaduje sa pritom vytvorenie takej zmesi, ktorá obsahuje
aspoň 30% čistiacich a dezinfekčných zložiek a minimum alergénov.
1.Nájdite minimum funkcie f (u,v) =u2+2u−4uv+5v2−8v+5 metódou Neldera
a Meada ( 4 kroky ). Vrcholy východiskového simplexu :
(1.9659,1.2588);(1.2588,1.9659);(1,1).
1. Riešte úlohu: extr f x y x y
x y
( , ) 4 2
,
= + pri splnení ohraničenia: x2 + y2 = 2 (extr znamená
minimum alebo maximum). Ako sa zmení optimálna hodnota f(x,y), ak sa pravá strana
ohraničenia zmení na 1. Nakreslite.
Prípravok na podlahu má vzniknúť vhodnou kombináciou troch surovín, obsahujúcich
čistiace - C, dezinfekčné - D a neutrálne - N, ako aj alergiu -vyvolávajúce - A zložky; ich
obsah je uvedený v tabuľke. Požaduje sa pritom vytvorenie takej zmesi, ktorá obsahuje
aspoň 30% čistiacich a dezinfekčných zložiek a minimum alergénov.
Kľúčové slová:
optimalizácia
zlatý rez
funkcia
ťažisko
ohraničenie
minimum funkcie
extrém
matematika
Obsah:
- Vypracovanie - Zadanie č.1.pdf
Vypracovanie - Zadanie č.2.pdf
Vypracovanie - Zadanie č.3.pdf
Vypracovanie - Zadanie č.4.pdf