Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 118
projektov
Otázky na aplikovanú matematiku
«»
| Prípona |
Typ výpočet |
Stiahnuté 6 x |
| Veľkosť 4,0 MB |
Jazyk slovenský |
ID projektu 39369 |
| Posledná úprava 25.01.2012 |
Zobrazené 2 016 x |
Autor: pdzurbal |
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
10 Kreditov - kvalita:
84,9% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Technická univerzita v Košiciach
- Fakulta:Fakulta výrobných technológií so sídlom v Prešove
- Kategória:Technika » Informatika
- Predmet:Aplikovaná matematika
- Študijný program:Riadenie výroby
- Ročník:4. ročník
- Formát:PDF dokument (.pdf)
- Rozsah A4:40 strán
1. Charakterizujte chyby pri numerických výpočtoch
Každá numerická úloha, je zaťažená 3 druhmi chýb:
1.Chybami vstupných dát, tzv. diskretizačnými chybami, ktoré môžu vznikať ako chyby z merania vstupných údajov. Vo všeobecnosti vstupné hodnoty numerickej úlohy nie sú dané presne. Miera podmienenosti je definovaná tzv. číslom podmienenosti úlohy, ináč vyjadrené je to pomer „relatívnej chyby výstupu ku relatívnej chybe vstupu“.
2.Chybou mtetódy, tj.j chybou aproximácie matematickej úlohy úlohou numerickou. Pri použití numerickej metódy nahradzujeme v skutočnosti všetky nekonečné procesy konečným procesom.
3.Zaokruhľovacími chybami, ktoré vznikajú v priebehu výpočtov zaokrúhľovaním medzivýsledkov.
...
2. Pojem aproximácie funkcie, interpolácie
Často v úlohách numerickej matematiky a pre riešenie inžinierskych úloh potrebujeme nahradiť danú funkciu f(x) nejakou inou funkciou φ(x), ktorej priebeh na inom intervale napodobňuje chovanie funkcie f(x) a ktorá má tú vlastnosť, že matematicky sa ľahko spracováva. Túto funkciu φ(x) nazávame aproximáciu (pribižením) funkcie f(x). Na použitie aproximácie nás vedú rôzne dôvody. Napr. výpočet fukčných hodnôt elementárnych funkcií na počítačoch sa realizuje použitím takých aproximácií φ(x), ktorých hodnoty sa dajú vypočítať aritmetickými operáciami. Iným typickým príkladom sú numerické metódy pre výpočet určitého integrálu z funkcie f(x). V tomto prípade nahradzujeme funkciu f(x) funkciou φ(x), ktorá sa ľahko integruje (napr. polynómom) Ak uvažujeme spojité funkcie, najšastejšie volíme...
Každá numerická úloha, je zaťažená 3 druhmi chýb:
1.Chybami vstupných dát, tzv. diskretizačnými chybami, ktoré môžu vznikať ako chyby z merania vstupných údajov. Vo všeobecnosti vstupné hodnoty numerickej úlohy nie sú dané presne. Miera podmienenosti je definovaná tzv. číslom podmienenosti úlohy, ináč vyjadrené je to pomer „relatívnej chyby výstupu ku relatívnej chybe vstupu“.
2.Chybou mtetódy, tj.j chybou aproximácie matematickej úlohy úlohou numerickou. Pri použití numerickej metódy nahradzujeme v skutočnosti všetky nekonečné procesy konečným procesom.
3.Zaokruhľovacími chybami, ktoré vznikajú v priebehu výpočtov zaokrúhľovaním medzivýsledkov.
...
2. Pojem aproximácie funkcie, interpolácie
Často v úlohách numerickej matematiky a pre riešenie inžinierskych úloh potrebujeme nahradiť danú funkciu f(x) nejakou inou funkciou φ(x), ktorej priebeh na inom intervale napodobňuje chovanie funkcie f(x) a ktorá má tú vlastnosť, že matematicky sa ľahko spracováva. Túto funkciu φ(x) nazávame aproximáciu (pribižením) funkcie f(x). Na použitie aproximácie nás vedú rôzne dôvody. Napr. výpočet fukčných hodnôt elementárnych funkcií na počítačoch sa realizuje použitím takých aproximácií φ(x), ktorých hodnoty sa dajú vypočítať aritmetickými operáciami. Iným typickým príkladom sú numerické metódy pre výpočet určitého integrálu z funkcie f(x). V tomto prípade nahradzujeme funkciu f(x) funkciou φ(x), ktorá sa ľahko integruje (napr. polynómom) Ak uvažujeme spojité funkcie, najšastejšie volíme...
Kľúčové slová:
aplikovaná matematika
Obsah:
- 1. Charakterizujte chyby pri numerických výpočtoch
2. Pojem aproximácie funkcie, interpolácie
3. Interpolácia polynómami (Newtonov interpolačný polynóm – lineárna, kvadratická interpolácia)
4. Popíšte princíp algoritmu Newtonovho interpolačného polynómu
5. Lagrangeov interpolačný polynóm
6. Princíp algoritmu Lagrangeovho interpolačného polynómu
7. Metóda najmenších štvorcov (lineárna, hyperbolická závislosť), index korelácie
8. Princíp algoritmu metódy najmenších štvorcov
9. Linearizácia nelineárnych vzťahov (popíšte postup)
10. Popíšte metódu delenia intervalu
11. Princíp algoritmu delenia intervalu (vývojový diagram)
12. Newtonova metóda (dotyčníc, podmienka pre ukončenie iteračného procesu, odhad chyby iterácie)
13. Princíp algoritmu Newtonovej metódy (vývojový diagram)
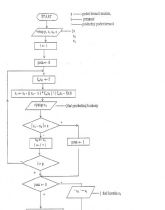
14. Metóda regula falsi (iteračný vzťah pre výpočet postupnosti iterácií, podmienka pre ukončenie iterácii)
15. Princíp metódy algoritmu regula falsi
16. Metóda jednoduchej iterácie (veta o konvergencii iterácie, koeficient kontrakcie, kritérium pre ukončenie výpočtu)
17. Princíp algoritmu metódy jednoduchej iterácie
18. Princíp algoritmu kombinovanej metódy Newton-Regula falsi
19. Podstata Gaussovej eliminačnej metódy
20. Algoritmus Gaussovej eliminačnej metódy (hrubý vývojový diagram s popisom funkcie programov)
21. Podstata Jacobiho a Gauss-Seidlovej metódy (približné riešenie, iteračný proces, iteračná metóda, konvergencia iteračného procesu)
22. Popis algoritmu Jacobiho metódy
23. Popis algoritmu Gauss-Seidlovej metódy
24. Newtonova metóda riešenia sústavy nelineárnych rovníc (SNL)
25. Algoritmus Newtonovej metóda
26. Podstata aproximácie funkcie, interpolácie
27. Numerický výpočet určitého integrálu (lichobežníková metóda)
28. Uveďte algoritmus (princíp) lichobežníkovej metódy
29. Simpsonova metóda
30. Princíp algoritmu Simpsonovej metódy
31. Problém numerického riešenia diferenciálnych rovníc (Cauchyho úloha, Lipschitzova podmienka, vstupné dáta zač. úlohy)
32. Eulerová metóda (rekurentný vzťah)
33. Algortimues Eulerovej metódy
34. Rungeho-Kuttova metóda (podstata metódy, R-K vzťahy pre štyri aproximácie)
35. Algoritmus Rungeho-Kuttovej metódy
36. Pojem štatistického súboru, prvku, znaku a základné spracovanie štatistického súboru
39. Grafické znázornenie štatistického súboru
40. Bayesova teoréma (veta o hypotézach)
41. Pojem náhodnej premennej (diskrétna a spojitá náhodná premenná)
42. Číselné charakteristiky náhodnej premennej (mat. nádej, modus, medián, disperzia)
46. Normované normálne rozdelenie, binomické rozdelenie (Poissonove)
49. Postup pri testovaní hypotéz
50. Dixonov neparametrický test a Grubbsov parametrický test
51. Pearsonov test 2 a Kolmogorov-Smirnovov test
54. Nelineárne regresné modely (polynominálne, exponencionálne modely)
Pridaj projekt
Pridaj projekt a získaj kredity za stiahnutie. S kreditmi možeš sťahovať iné projekty. Je to jednoduché :)
Najčastejšie
Zobraz
Odporúčame
Zadania-seminarky.sk
2006 - 2024 © všetky práva vyhradené