Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 091 projektov
0 nových
Vlastnosti funkcií s deriváciou a priebeh funkcie
«»
| Prípona |
Typ výpočet |
Stiahnuté 92 x |
| Veľkosť 0,3 MB |
Jazyk slovenský |
ID projektu 2992 |
| Posledná úprava 30.03.2017 |
Zobrazené 2 735 x |
Autor: - |
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
2 Kreditov - kvalita:
77,1% -
Stiahni
- Pridaj na porovnanie
- Univerzita:-
- Fakulta:-
- Kategória:Prírodné vedy » Matematika
- Predmet:Matematika
- Študijný program:-
- Ročník:-
- Formát:PDF dokument (.pdf)
- Rozsah A4:12 strán
7.1 Úvodné tvrdenia
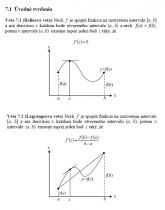
Veta 7.1 (Rolleova veta) Nech f je spojitá funkcia na uzavretom intervale [a, b] a má deriváciu v každom bode otvoreného intervalu (a, b) a nech f(a) = f(b), potom v intervale (a, b) existuje aspoň jeden bod c taký, že
Veta 7.2 (Lagrangeova veta) Nech f je spojitá funkcia na uzavretom intervale [a, b] a má deriváciu v každom bode otvoreného intervalu (a, b), potom v intervale (a, b) existuje aspoň jeden bod c taký, že
Veta 7.1 (Rolleova veta) Nech f je spojitá funkcia na uzavretom intervale [a, b] a má deriváciu v každom bode otvoreného intervalu (a, b) a nech f(a) = f(b), potom v intervale (a, b) existuje aspoň jeden bod c taký, že
Veta 7.2 (Lagrangeova veta) Nech f je spojitá funkcia na uzavretom intervale [a, b] a má deriváciu v každom bode otvoreného intervalu (a, b), potom v intervale (a, b) existuje aspoň jeden bod c taký, že
Kľúčové slová:
konkávnosť
konvexnosť
inflexný bod
lokálne extrémy
Lagrangeova veta
Obsah:
- 7. Vlastnosti funkcií s deriváciou a priebeh funkcie
7.1 Úvodné tvrdenia
7.2 Monotónnosť a lokálne extrémy
7.3 Konvexnosť, konkávnosť a inflexné body
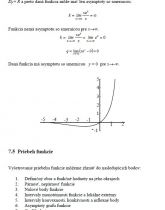
7.4 Asymptoty grafu funkcie
7.5 Priebeh funkcie
Cvičenia
Pridaj projekt
Pridaj projekt a získaj kredity za stiahnutie. S kreditmi možeš sťahovať iné projekty. Je to jednoduché :)
Najčastejšie
Zobraz
Odporúčame
Zadania-seminarky.sk
2006 - 2024 © všetky práva vyhradené