Hľadaj
Zobraz:
Univerzity
Kategórie
Rozšírené vyhľadávanie
45 146
projektov
Zadanie č.2 - Časové systémy
| Prípona .zip |
Typ výpočet |
Stiahnuté 15 x |
| Veľkosť 0,4 MB |
Jazyk slovenský |
ID projektu 45279 |
| Posledná úprava 07.10.2014 |
Zobrazené 1 209 x |
Autor: testamentALBUSAdambl |
 Zdieľaj na Facebooku
Zdieľaj na Facebooku |
||
| Detaily projektu | ||
- cena:
0 Kreditov - kvalita:
77,3% -
Stiahni
- Pridaj na porovnanie
- Univerzita:Slovenská technická univerzita v Bratislave
- Fakulta:Stavebná fakulta
- Kategória:Technika » Stavebníctvo
- Predmet:Sférická astronómia a kozmická geodézia
- Študijný program:Geodézia a kartografia
- Ročník:3. ročník
- Formát:Archív súborov (.zip)
- Rozsah A4:1 strán
Zadanie č. 2
ČASOVÉ SYSTÉMY
1. Vyriešte úlohu o polohe hviezdy na sfére podľa individuálneho zadania, ak sú známe jej rovníkové súradnice a hviezdny čas s.
2. Rozhodnite, v akom poradí nastanú časy S1 a S2 v dvoch rozdielnych dátumoch d1, d2 = d1 + 3 mesiace. Dátum d1 použite z úlohy 5. Ak je poradie rovnaké v oboch dátumoch, uveďte najbližší dátum k d1, v ktorom by sa zmenilo.
Nasledujúce 4 úlohy vyriešte pre stanovisko so zadanou zemepisnou dĺžkou L.
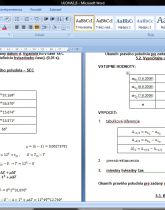
3. Vypočítajte hodinový uhol t hviezdy H(a) v okamihu SEČ v zadanom dátume d. Presnosť je (0,001 s)
4. Vypočítajte SEČ (0,001 s), v ktorom dosiahne hviezda H(a) hodinový uhol t. Riešte pre zadaný dátum d.
5. Vypočítajte okamih pravého poludnia pre zadaný dátum d. Vyjadrite ho v čase SEČ (pomocou časovej rovnice E) a s (pomocou definície hviezdneho času). (0,01 s).
6. V akom čase SEČ a s dosiahne Slnko zadanú polohu (definovanú hodinovým uhlom tO) v zadanom dátume. Použite postup ako v úlohe 5. a SEČ skontrolujte transformáciou s ® SEČ. Presnosť (0,01 s). Úlohu nakreslite.
7. Zo zoznamu úloh vyriešte zadanú dvojicu.
ČASOVÉ SYSTÉMY
1. Vyriešte úlohu o polohe hviezdy na sfére podľa individuálneho zadania, ak sú známe jej rovníkové súradnice a hviezdny čas s.
2. Rozhodnite, v akom poradí nastanú časy S1 a S2 v dvoch rozdielnych dátumoch d1, d2 = d1 + 3 mesiace. Dátum d1 použite z úlohy 5. Ak je poradie rovnaké v oboch dátumoch, uveďte najbližší dátum k d1, v ktorom by sa zmenilo.
Nasledujúce 4 úlohy vyriešte pre stanovisko so zadanou zemepisnou dĺžkou L.
3. Vypočítajte hodinový uhol t hviezdy H(a) v okamihu SEČ v zadanom dátume d. Presnosť je (0,001 s)
4. Vypočítajte SEČ (0,001 s), v ktorom dosiahne hviezda H(a) hodinový uhol t. Riešte pre zadaný dátum d.
5. Vypočítajte okamih pravého poludnia pre zadaný dátum d. Vyjadrite ho v čase SEČ (pomocou časovej rovnice E) a s (pomocou definície hviezdneho času). (0,01 s).
6. V akom čase SEČ a s dosiahne Slnko zadanú polohu (definovanú hodinovým uhlom tO) v zadanom dátume. Použite postup ako v úlohe 5. a SEČ skontrolujte transformáciou s ® SEČ. Presnosť (0,01 s). Úlohu nakreslite.
7. Zo zoznamu úloh vyriešte zadanú dvojicu.
Kľúčové slová:
rovníkové súradnice
hviezdny čas
hodinový uhol
SEČ
časová rovnica
Obsah:
- Mathcad-y obsahuju numericke riešenia uloh a docx-i technicku spravu.
Zdroje:
- Sférická astronómia a kozmická geodézia, Ladislav Husár